TensorFlowで実践ディープラーニング（その１）

深層学習（ディープラーニング）とは何なのか

人工知能（AI）は、「機械学習」と「深層学習」に分類されます。簡単に言ってしまえば、「機械学習」を進化させたものが「深層学習」です。これだけ聞いても、いったい何のことやらよくわかりませんよね。

人工知能（AI）は、基本的にビッグデータを入力して、そのデータに含まれる規則性やパターンを見つけたり、分類や予測する技術のことを言います。

その規則性やパターンのことを特徴量と言い、人間があらかじめ定義した特徴を使用して処理するものが「機械学習」、与えられたデータから自動的に特徴を抽出して処理するのが「深層学習」と言うことができます。

人間は、五感で得られた情報を色、形、臭いや味などを脳に記憶する学習をしています。「深層学習」の概念は、人間の学習行動と同じと言えます。つまり、脳の学習の仕組みを模造したものが「深層学習」なのです。

人間の脳は、膨大な数のニューロンという神経細胞で構成されています。ニューロンは、情報処理と情報伝達に特化した細胞であり、この細胞同士が複雑に結合して情報伝達し合うことで、人間の記憶力や思考力が発揮されます。

ニューロンの結合により形成されたネットワークのことを、「ニューラルネットワーク」と言います。「深層学習」の分野における「ニューラルネットワーク」は、入力層、隠れ層及び出力層の３つの層を形成し、学習と予測を行いますが、単純に３つの層しかないので、人間の脳のような複雑な学習や予測は難しいですす。

しかしながら、隠れ層を何層も重ねて人間の脳のような複雑なニューロンの結合を模擬することで、高度な学習と高い認知能力を得ることができるようになります。この多層構造型ニューラルネットワークのことを「深層学習（ディープラーニング）」と呼んでいます。

今回は、TensorFlow（テンソルフロー）を使って基礎的な深層学習（ディープラーニング）を実践していきます。TensorFlowは、Google社が開発しオープンソースとして公開されている深層学習のフレームワークです。

プログラミング言語は、C言語、C++、JavaやPythonに対応しており、CPUだけではなくGPGPUを使用することも可能なため、ビッグデータを高速で学習することも可能です。

TensorFlow（テンソルフロー）は、入力されたデータをテンソルとして処理します。テンソルとは、一言で言うと多次元配列のことです。テンソルの世界では、スカラーは０階のテンソル、ベクトルは１階のテンソル、２次元配列（行列）は２階のテンソル、３次元配列は３階のテンソルと表現されます。

私たちの世界は、立体（３次元）＋時間で構成されているので４階のテンソルと言うことができます。

ロジスティック回帰分析

TensorFlowとPythonを使って深層学習を実践していきます。人工知能でよく利用されるアヤメのデータセットを使用して、ロジスティック回帰分析について学習していきます。

ロジスティック回帰分析は、発生確率を予測する多変量解析方法であり、量を予測する線形回帰分析とは全く異なる手法です。ロジスティック回帰分析は、線形分離が不可能な問題についても解を得ることが可能です。

ロジスティック回帰分析を処理するpythonコードは以下の通りです。

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
import tensorflow as tf

#①データの読込み
#アヤメCSVデータの読込み
csv = pd.read_csv('iris.csv')
iris_class = {'Iris-setosa': [1,0,0], 'Iris-versicolor': [0,1,0], 'Iris-virginica': [0,0,1]}
csv["Name"] = csv["Name"].apply(lambda x : np.array(iris_class[x]))
csv_data = csv[["SepalLength","SepalWidth","PetalLength","PetalWidth"]]
csv_label = csv["Name"]

#学習用データと訓練用データに分割する
train_data, test_data, train_label, test_label = \
train_test_split(csv_data, csv_label, test_size=0.3, shuffle=True)

train_data = train_data.reset_index(drop=True)
train_label = train_label.reset_index(drop=True)
test_data = test_data.reset_index(drop=True)
test_label = test_label.reset_index(drop=True)

#②データフローグラフ（モデル）の設定
#データを入れるプレースホルダを宣言
x = tf.placeholder(tf.float32, [None, 4], name="x")
y_ = tf.placeholder(tf.float32, [None, 3], name="y_")
#変数宣言"
W = tf.Variable(tf.zeros([4, 3]), name="W")
b = tf.Variable(tf.zeros([3]), name="b")
#ソフトマックス回帰を定義
y = tf.nn.softmax(tf.matmul(x, W) + b)

#③モデルの訓練設定
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(cross_entropy)

#④正解率を求める設定
predict = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(predict, tf.float32))
#セッション開始
with tf.Session() as sess:
  tw = tf.summary.FileWriter("log_dir", graph=sess.graph)
  #初期化
  sess.run(tf.global_variables_initializer())
  
  #⑤反復学習
  #学習データを用いて学習する
  fd = {x: train_data, y_: list(train_label)}
  for step in range(201):
    sess.run(train, feed_dict=fd)
    if step % 10 == 0:
      cre = sess.run(cross_entropy, feed_dict=fd)
      acc = sess.run(accuracy, feed_dict=fd)
      print("step=",step,"cross entropy=",cre,"accuracy=",acc )
  
  #⑥試験データによる精度評価
  #試験データを用いて正解率を求める
  fd = {x: test_data, y_: list(test_label)}
  
  acc = sess.run(accuracy, feed_dict=fd)
  print('正解率=','{0:.2f}'.format(acc))

では、実際に学習状況を見てみましょう。

step= 0 cross entropy= 1.0969 accuracy= 0.352381
step= 10 cross entropy= 1.08234 accuracy= 0.352381
step= 20 cross entropy= 1.07152 accuracy= 0.352381
step= 30 cross entropy= 1.06304 accuracy= 0.352381
step= 40 cross entropy= 1.05567 accuracy= 0.352381
step= 50 cross entropy= 1.04867 accuracy= 0.352381
step= 60 cross entropy= 1.04165 accuracy= 0.361905
step= 70 cross entropy= 1.03452 accuracy= 0.419048
step= 80 cross entropy= 1.02725 accuracy= 0.647619
step= 90 cross entropy= 1.0199 accuracy= 0.67619
step= 100 cross entropy= 1.01255 accuracy= 0.67619
step= 110 cross entropy= 1.00525 accuracy= 0.67619
step= 120 cross entropy= 0.998091 accuracy= 0.67619
step= 130 cross entropy= 0.991113 accuracy= 0.67619
step= 140 cross entropy= 0.984363 accuracy= 0.67619
step= 150 cross entropy= 0.977871 accuracy= 0.67619
step= 160 cross entropy= 0.971656 accuracy= 0.67619
step= 170 cross entropy= 0.965729 accuracy= 0.67619
step= 180 cross entropy= 0.960091 accuracy= 0.67619
step= 190 cross entropy= 0.954739 accuracy= 0.67619
step= 200 cross entropy= 0.949666 accuracy= 0.67619
正解率= 0.64

このトライアルでは、学習用データについて２００回繰り返し学習を行っています。そして学習回数毎に交差エントロピー誤差（cross entropy）と正解率（accuracy）を出力しています。

初度の学習段階（step= 0）では、35.23%の正解率でしたが、中間付近（step= 90付近）では、正解率が67%ぐらいまで向上していることがわかります。ただし、学習の後半部分では正解率が向上していません。最終的な正解率は、64%に留まりました。

次に学習回数を３万回まで増やしてみましょう。

step= 0 cross entropy= 1.09732 accuracy= 0.380952
step= 1000 cross entropy= 0.824519 accuracy= 0.895238
step= 2000 cross entropy= 0.772611 accuracy= 0.961905
step= 3000 cross entropy= 0.740389 accuracy= 0.980952
step= 4000 cross entropy= 0.717518 accuracy= 0.980952
step= 5000 cross entropy= 0.700485 accuracy= 0.980952
step= 6000 cross entropy= 0.687353 accuracy= 0.980952
step= 7000 cross entropy= 0.676932 accuracy= 0.980952
step= 8000 cross entropy= 0.66846 accuracy= 0.980952
step= 9000 cross entropy= 0.661431 accuracy= 0.980952
step= 10000 cross entropy= 0.655497 accuracy= 0.980952
step= 11000 cross entropy= 0.650415 accuracy= 0.980952
step= 12000 cross entropy= 0.646008 accuracy= 0.980952
step= 13000 cross entropy= 0.642144 accuracy= 0.980952
step= 14000 cross entropy= 0.638725 accuracy= 0.980952
step= 15000 cross entropy= 0.635675 accuracy= 0.980952
step= 16000 cross entropy= 0.632934 accuracy= 0.980952
step= 17000 cross entropy= 0.630456 accuracy= 0.980952
step= 18000 cross entropy= 0.628202 accuracy= 0.980952
step= 19000 cross entropy= 0.626141 accuracy= 0.980952
step= 20000 cross entropy= 0.624249 accuracy= 0.980952
step= 21000 cross entropy= 0.622504 accuracy= 0.990476
step= 22000 cross entropy= 0.620889 accuracy= 0.990476
step= 23000 cross entropy= 0.619389 accuracy= 0.990476
step= 24000 cross entropy= 0.617991 accuracy= 0.990476
step= 25000 cross entropy= 0.616684 accuracy= 0.990476
step= 26000 cross entropy= 0.61546 accuracy= 0.990476
step= 27000 cross entropy= 0.61431 accuracy= 0.990476
step= 28000 cross entropy= 0.613227 accuracy= 0.990476
step= 29000 cross entropy= 0.612206 accuracy= 0.990476
step= 30000 cross entropy= 0.61124 accuracy= 0.990476
正解率= 0.98

２万回超えたあたりで予測精度が99%に到達しました。テストデータによる交差検証の正解率も98%に達しています。ニューラルネットワークにおいては、学習回数が予測精度を決定する重要な要素であることが確認できましたね。

交差エントロピー誤差とは、簡単に説明すると正解と予測の２つの確率分布がどの程度違うのかを表した量のことです。ディープラーニングの世界では、交差エントロピー誤差をいかに小さくするかに対するアプローチが、予測精度を向上させるための鍵となります。

アルゴリズムを理解する

上記のアルゴリズムは、入力値と出力値が以下のような関係の構造で成り立っています。

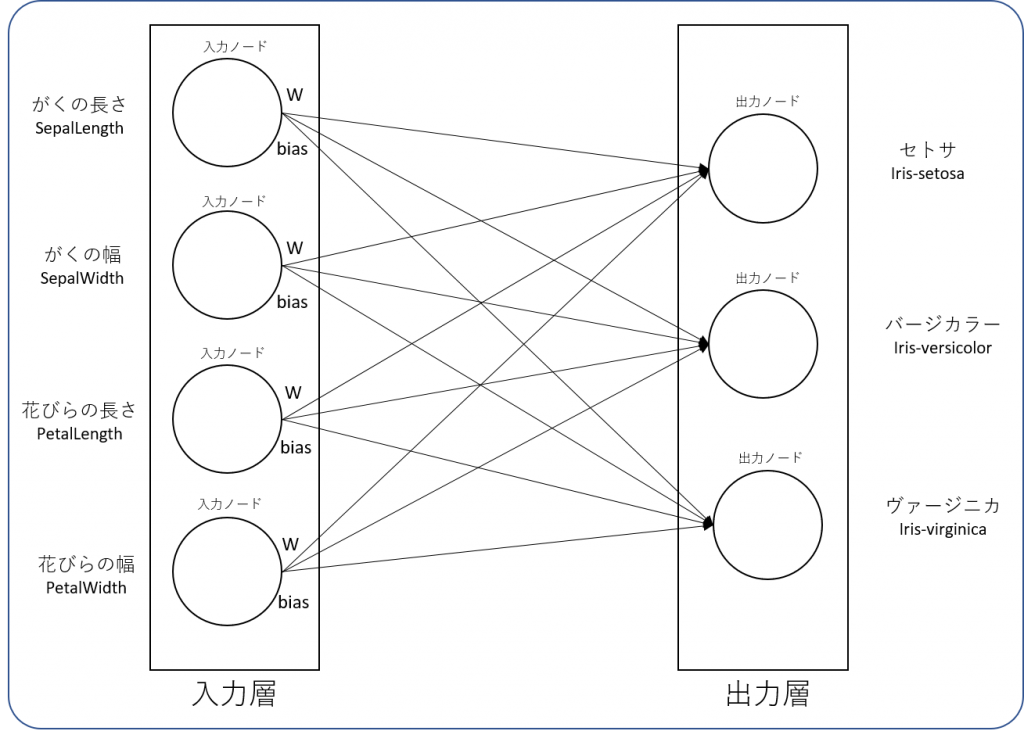
入力ノードは全ての出力ノードに接続されているため、合計で１２本の矢印が表現されています。TensorFlowは、この矢印の本数と同じ数だけの重み（Weight）と誤差（Bias）を学習しています。

上記の場合は、入力層と出力層の間に隠れ層（Hidden Layer）がない非多層構造型ニューラルネットワークになっていますが、ディープラーニングを学ぶ上でニューラルネットワークの基本を押さえておくことはとても重要です。

では、pythonコードについて分解して説明していきます。

TensorFlowのpythonスクリプトは、以下の流れで構成されています。
　①データの読込み
　②データフローグラフ（モデル）の設定
　③モデルの訓練設定
　④正解率を求める設定
　⑤反復学習
　⑥試験データによる精度評価

これ以降は、「②データフローグラフ（モデル）の設定」から「⑥試験データによる精度評価」について説明していきます。

#②データフローグラフ（モデル）の設定
#データを入れるプレースホルダを宣言
x = tf.placeholder(tf.float32, [None, 4], name="x")
y_ = tf.placeholder(tf.float32, [None, 3], name="y_")
#変数宣言"
W = tf.Variable(tf.zeros([4, 3]), name="W")
b = tf.Variable(tf.zeros([3]), name="b")
#ソフトマックス回帰を定義
y = tf.nn.softmax(tf.matmul(x, W) + b)

TensorFlowでは、モデル（学習器）のことをグラフ（Graph）と呼ぶこともあります。このセクションでは、グラフに入力する説明変数（x）と目的変数（y_）をプレースホルダーという入れ物として準備しています。

プレースホルダーは、型や配列に関する単なる入れ物の定義であるため、この段階ではデータは何も入っていません。値は、Session.run()メソッドの引数feed_dictに辞書型で指定することにより入力されます。

説明変数（x）は、「がく」と「花びら」の「長さ」と「幅」の４つの要素で構成されたデータなので、 プレースホルダの配列は[None, 4]と設定します。

目的変数（Y_）は、３種類のアヤメを表しているので、プレースホルダの配列は[None, 3]と設定しています。なお、「None」は、入力するデータ数（標本数）を表すため任意サイズの配列として設定します。

重み（W）は、入力側４つと出力側３つの配列を「0:Zero」で初期化します。バイアス（b）は、出力側に加算されるものなので３つの配列を「0:Zero」で初期化します。

次にソフトマックス関数を使用したロジスティック回帰を宣言します。ソフトマックス関数は以下のようなグラフとなっています。

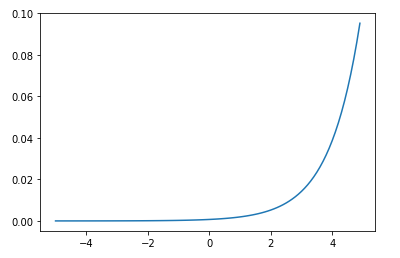
ソフトマックス関数は、以下のような性質があります。
　(1)　０　＜　Yi　＜　１
　(2)　Y1 ＋　・・・　＋　Yn ＝　１

ソフトマックス関数で求められるものは確率であり、１に近いほど尤もらしいことを表しています。ソフトマックス関数に与えられるものは、配列の説明変数（x）と重み（W）の積にバイアス（b）を加算したものです。配列の積は、matmul()メソッドで処理されています。

#③モデルの訓練設定
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(cross_entropy)

モデルの訓練設定では、損失関数オプティマイザの設定を行います。損失関数とは、２つの値を小さくする関数のことを言います。

TensorFlowには、損失関数を最小限に抑制するため、各変数の値をゆっくりと変化させるオプティマイザが準備されています。損失関数オプティマイザの設定は、optimizer.minimize()メソッドで行い、この実験では、交差エントロピー誤差を入力値として設定しています。

#④正解率を求める設定
predict = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(predict, tf.float32))

tf.equal()メソッドは、与えられた２つのベクトルが一致しているかを検査する設定です。yには予測結果、y_は正解が与えられています。

tf.cast()メソッドは第１引数を第２引数の型に型変換する方法を設定しています。

tf.reduce_mean()メソッドは、平均を計算する設定です。

with tf.Session() as sess:
tw = tf.summary.FileWriter("log_dir", graph=sess.graph)
#初期化
sess.run(tf.global_variables_initializer())
#⑤反復学習
#学習データを用いて学習する
fd = {x: train_data, y_: list(train_label)}
for step in range(201):
sess.run(train, feed_dict=fd)
if step % 10 == 0:
cre = sess.run(cross_entropy, feed_dict=fd)
acc = sess.run(accuracy, feed_dict=fd)
print("step=",step,"cross entropy=",cre,"accuracy=",acc )

TensorFlowの処理は、Session()メソッドの中で実行されます。ニューラルネットワークの学習では、繰り返し学習（反復学習）することにより予測精度を向上させています。

この実験では、２００回の反復学習を実行させています。sess.run(train, feed_dict=fd)メソッドの部分が実際に学習を行っている部分であり、第１引数に③モデルの訓練設定で設定した訓練設定を与えています。

第２引数には、辞書型リストで訓練用データ（説明変数と目的変数）を与えています。ここでは便宜上、fd変数に辞書型リストを代入しておいて、feed_dictにfd変数を渡しています。１０回ごとの学習状態を観察するため、交差エントロピー誤差と正解率を標準出力させています。

#⑥試験データによる精度評価
#試験データを用いて正解率を求める
fd = {x: test_data, y_: list(test_label)}
acc = sess.run(accuracy, feed_dict=fd)
print('正解率=','{0:.2f}'.format(acc))

最後に、テスト用データを使用して正解率を求め、予測精度を確認しています。

TensorFlowの処理内容を可視化する

TensorFlowには、データの流れを可視化するTensorBoardというツールが準備されています。これを使うことにより、TensorFlowの処理を視覚的に理解することができます。

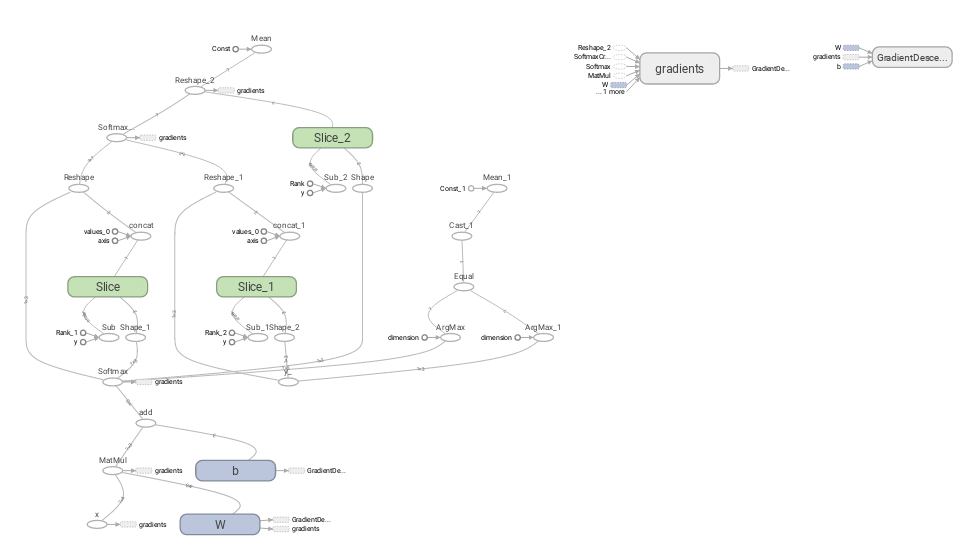
慣れないと少し難しいかもしれませんね。TensorFlowを可視化するには、以下の記述を追加します。

with tf.Session() as sess:
tw = tf.summary.FileWriter("log_dir", graph=sess.graph)

tf.summary.FileWriter()メソッドの第１引数は、TensorFlowのログを格納するディレクトリを指定します。セッションは、tf.Session() as sessと設定したので、第２引数にgraph=sess.graphと設定します。実行後、指定したディレクトリ内にTensorFlowのイベントログ（events.out.tfevents*）が出力されているはずです。

実際に可視化するには、以下のコマンドを実行してブラウザに出力させる必要があります。

tensorboard --logdir=./log_dir

logdirオプションに渡すディレクトリパスについては、絶対パスでも相対パスでも問題ないようです。http://localhost:6006/にアクセスするとTensorBoardのダッシュボードが表示されますので、「GRAPHS」タブを押すと上記のような図が表示されます。

今回のまとめ

今回は、TensorFlowを使用して簡単なディープラーニングを実践してみました。scikit-learnと比べるとpythonコードの記述も増えて、記述内容も複雑になっていることが体験できました。

しかしながら、深層学習（ディープラーニング）のスキルを習得する上では、初歩的な事からしっかりと学習することが、今後のAI学習のモチベーションの維持に欠かすことができません。

今回の実験では、入力層と出力層しかない単層構造のニューラルネットワークについて実験しましたが、これに隠れ層（Hidden Layer）を追加すれば、多層構造のニューラルネットワークを構築できます。